Session 1   Getting Started

1  Setting Up

1.1  Installing the Toolbox

In this tutorial, you will use the Toolbox for writing algorithms and running tools to check them.  The Toolbox is a rather heavyweight IDE (Integrated Development Environment), and you may dislike it.  However, it has many useful features that make learning (and using) PlusCal and its tools easier.  If you hate the idea of using the Toolbox, click here to see why that shouldn't stop you from following this tutorial.

Instructions for downloading and installing the Toolbox on your computer can be found on the TLA+ web site.  You won't need to install pdflatex unless you want to pretty-print your algorithms, and you can ignore the section on using the Toolbox.  All you need to know about using the Toolbox in the tutorial will be explained.  Now, just install and run the Toolbox.  Pay no attention to what it shows you.

If you have previously installed the Toolbox, update it if necessary so your version is at least as recent as 1.7.1.

1.2  Downloading the Files

You need to download files containing the examples that you will use with the Toolbox.  They are all contained in a zip file.  Create a folder (directory), download the zip file from here, and extract its files into that folder.  You will be modifying those files during the tutorial, so you should keep copies of them in another directory so you can easily restore a file you've been using to its original version.

2  Data Types

The data types of PlusCal are the data types of TLA+.  They include any data type you can describe with mathematics.  We'll start by learning about some of the basic ones.

We'll use the TLC model checker to play with TLA+ data types.  A PlusCal algorithm appears in a TLA+ specification, which usually consists of a single file containing the algorithm.  We run TLC on that specification.  Since we're not going to look at algorithms yet, we will run TLC on an essentially empty specification.  That specification is named Session1 and is in the file Session1.tla that is among the files you've just downloaded.  We begin by opening it.

2.1  Opening a Specification

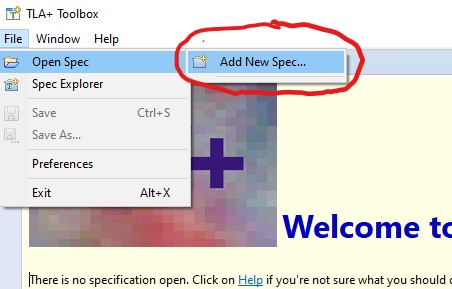
In the upper left-hand corner of the Toolbox window, click on File, then on Open Spec, and then Add New Spec.

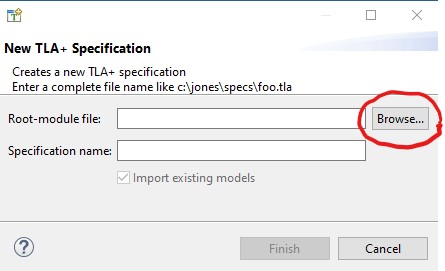
This raises the specification-chooser window shown here on the left.  Click on the Browse button.  This raises a file browser window for choosing a file.  Use it to find and select the file Session1.tla that you downloaded.

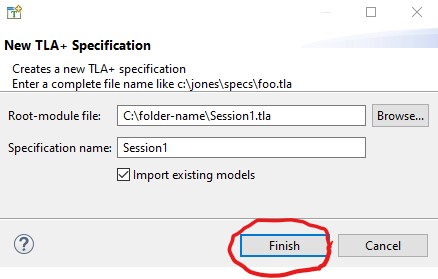
Click on the Finish button on the specification-chooser window.  You should ignore what now appears in the Toolbox window, but you may want to close the Spec Explorer tab by clicking on this symbol in its upper-right corner.

2.2  Opening a Model

TLC is run on what we call a model, which tells it exactly what to check and gives it some instructions on how it should be run.  Specification Session1 comes with a model having the clever name Model_1.

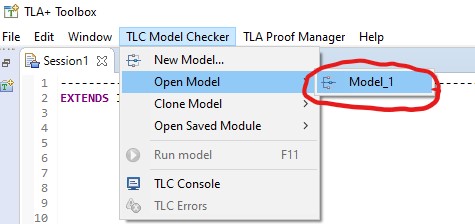Open that model by clicking on TLC Model Checker on the Toolbox's top menu bar, then clicking Open Model.  This causes the Toolbox to create a tab for Model_1 and open the Model Checking Results sub-tab.

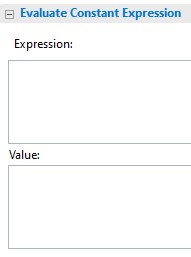This Evaluate Constant Expression section is the only part of the Toolbox that concerns us now.  It turns TLC into a calculator for TLA+ data types.  Try it out.  Type 2+2 in the Expression section.  Now run TLC by clicking on this icon in the upper-left corner of the sub-tab.  TLC should run for a couple of seconds and write 4 in the Value section.  (Those couple of seconds are a constant startup delay and are insignificant when using TLC to check a real algorithm.)

Data structures and operators on them are introduced throughout the tutorial as needed.  By the end of the tutorial, you will have seen most of the ones you will need.  All of them can be found in the Constant Operators and Operators Defined in Standard Modules sections of this document.  Below are the ones we will start with.

2.3  Numbers and Strings

Numbers

TLA+ has integers like 42 and -123.  It has the usual arithmetic operators +, -, and * (multiplication).  (Don't worry about division yet.)  There are the usual equality and inequality operations =, <, and >.  In TLA+,  ≤  and  ≥  are typed =< and >=, and  ≠  is typed either /= or #.  Try them out by having TLC evaluate some expressions. For example, have it evaluate each the following three expressions by copying and pasting it into the Expression section and running TLC on it.

   -8 + 2*9 
   2*3 = 5+1 
   3-2 >= 3+2   

Integers in TLA+ are really integers, not 32- or 128-bit numbers.  In TLA+, this formula equals TRUE:

99999999999999999999 + 99999999999999999999 = 199999999999999999998

The TLAPS theorem prover can prove that it's true.  However, TLC can't handle numbers that big.  The version of TLC now on my computer can only handle integers from -2147483647 through 2147483647.  But you shouldn't worry about that.  When writing algorithms in PlusCal, you almost always want to think in terms of integers.  That they will be implemented in terms of a bounded set of numbers is one of the lower-level details that you will want to ignore.

Syntax Errors

If you type a syntactically incorrect expression in the Expression field, the Toolbox will raise an error window reporting:

No error information.

Strings

TLA+ also has strings like "ab_3X" and "" (the empty string).  PlusCal and TLA+ were designed for writing concurrent algorithms, which rarely manipulate strings.  Strings are meant to be used only as names, and the TLA+ operators provide no way to access the characters in a string.  (TLA+ has no built-in character data type.)  If you want to debug a string processing algorithm with PlusCal, you'll probably want to use some other way to represent strings.

What should evaluating the expression 1 = "a" produce?  The obvious answer is FALSE, since numbers and strings are different.  But I wouldn't have asked the question if the answer were obvious.  So, let TLC evaluate it and then click here to show the explanation of what happened.

Attempted to check equality of integer 1 with non-integer: "a" 

2.4  Tuples

Here is a tuple <<"a",-3,"bc">> with three elements.  Its first and third elements are strings and its second element is a number.  In TLA+, a tuple t is an array whose  i ^th  element is t[i].  For example, <<"a",-3,"bc">>[1] equals "a".  (You may want to click here for an explanation of why TLA+ numbers tuple elements starting at 1 rather than 0.)  The length of (number of elements in) a tuple t is written Len(t).  Thus, Len(<<"a",-3,"bc">>) equals 3.

Tuples are also called lists and (finite) sequences.  They are a very useful data type and there are operators for constructing and combining them that we'll see later.  When using TLC to evaluate expressions, you can save time by combining multiple expressions in a tuple instead of evaluating them individually.

2.5  Sets

A set is a collection of elements—nothing more and nothing less.  It is defined by saying what its elements are.  The set {1, 2, 3} is defined by saying it has three elements: 1, 2, and 3.  Since {3, 2, 1} also has those same three elements, it is the same set.  In other words, {3, 2, 1} equals {1, 2, 3}, which is the same as saying {3, 2, 1} = {1, 2, 3} equals TRUE.

The set {3, 3, 2, 1, 2} also has the three elements 1, 2, and 3.  Therefore it equals {1, 2, 3}.  I don't know what it would mean to say that a set has two copies of the element 3.  If the set {3, 3, 2, 1, 2} has two copies of 3, then the set {1, 2, 3} must also have two copies of 3, since it's the same set.  Saying that a set has two copies of an element is nonsense, so don't even think it.

The mathematical formula  e ∈ S  is true iff (if and only if)  S  is a set and  e  is an element of the set  S.  The symbol  ∈  is written \in in TLA+.  Thus, 2 \in {2,4,6} is true and 2 \in {1,3,5} is false.  The formula  e  ∉ S  is true iff  e  is not an element of  S.  The symbol  ∉  is written \notin in TLA+.  Thus 2 \notin {1,3,5} is true.

For any integers i and j, the expression i..j is the set of all integers k such that i =< k and k =< j are true.  For example (-2)..1 equals {-2,-1,0,1} and 4..2 equals {} (the empty set, which has no elements).

Of course, sets can contain any values as elements.  For example, {{"a","b"}, {"c"}} is a set with two elements: the sets {"a","b"} and {"c"}. 

We will use the following operators for sets S and T:

Union  ∪  -  written \cup in TLA+

S \cup T is the set of all elements that are in S or T or both.  For example, {1,2} \cup {2,4} equals {1,2,4}.

Intersection  ∩  -  written \cap in TLA+

S \cap T is the set of all elements that are in both S and T.  For example, {"a","b"} \cap {"b","c"} equals {"b"}.

Set Difference  \    (sometimes written -, but not in TLA+)

S \ T is the set of all elements that are in S and not in T.  For example, {1, 2} \ {2, 4} equals {1}.

Subset  ⊆  -  written \subseteq in TLA+

S \subseteq T is a Boolean valued expression that equals TRUE iff every element of S is an element of T.  For example, {"a", "c"} \subseteq {"a", "b", "c"} equals TRUE, and {"a", "c"} \subseteq {"b", "c", "d"} equals FALSE.

{<<1>>, <<2,2>>, <<3,3,3>>} \cup {<<1>>, <<1,2>>, <<1,2,3>>}
{{"a","b"}, {"a"}, {"b"}} \cap {{"a","b","c"}, {"a","b"}, {"a"}}
{"aa", "bb", "cc"} \ {"a", "b", "c"}
{1,1,2,2,3,3} \ {2, 3, 4}
{1,1,1} \subseteq {1,1,2,2}

<< {<<1>>, <<2,2>>, <<3,3,3>>} \cup {<<1>>, <<1,2>>, <<1,2,3>>}     ,
   {{"a","b"}, {"a"}, {"b"}} \cap {{"a","b","c"}, {"a","b"}, {"a"}} ,
   {"aa", "bb", "cc"} \ {"a", "b", "c"}                             ,
   {1,1,2,2,3,3} \ {2, 3, 4}                                        ,
   {1,1,1} \subseteq {1,1,2,2}
>>

TLA+ allows infinite sets.  Two infinite sets you might want to use are the set Int of all integers and the set Nat of all natural numbers (non-negative integers).  For example, what is the set  Nat \ -5..5 ?  You can't ask TLC to answer this for you because it can't evaluate an expression whose value is an infinite set.  But it doesn't have to compute that set to answer whether a number is an element of it.  For example, you can use it to evaluate this expression:  3 \in (Nat \ -5..5) .  So, you can figure out what the set  Nat \ -5..5  is by asking TLC to compute whether various numbers are in that set.

When writing algorithms, you will probably use an infinite set S only in an expression of the form e \in S.  TLC can evaluate such an expression for most of the infinite sets you're likely to use.  TLC is actually pretty good at evaluating an expression that equals a finite set, even if it contains infinite sets—for example, (-5..5) \cap Nat.  You might enjoy trying to use the sets and operators defined in this session, including Nat and Int, to write an expression that TLC can't evaluate even though it equals a finite set.  I haven't been able to do it.

You may be surprised by some apparently simple set expressions that TLC can't evaluate.  For example, tell TLC to evaluate the expression {1,"a"}.  It reports an error with an error message containing:

 Attempted to compare string "a" with non-string: 1 

2.6  Logic

Propositional Logic

Propositional logic is the arithmetic of the set {TRUE, FALSE} of Boolean values.  Its operators are defined as follows on the Boolean values P and Q:

Disjunction  ∨  -  pronounced or, written \/ in TLA+

P \/ Q is true iff either P or Q or both are true.  In other words:

TRUE \/ TRUE  equals TRUE        FALSE \/ TRUE equals TRUE
TRUE \/ FALSE equals TRUE        FALSE \/ FALSE equals FALSE

\/ is written || in some programming languages.

Conjunction  ∧  -  pronounced and, written /\ in TLA+

P /\ Q is true iff P and Q are both true.  In other words:

TRUE /\ TRUE  equals TRUE        FALSE /\ TRUE equals FALSE
TRUE /\ FALSE equals FALSE       FALSE /\ FALSE equals FALSE

/\ is written && in some programming languages.

Negation  ¬  -  pronounced not, written ~ in TLA+

~P is true iff P is false.  In other words:

~TRUE equals FALSE     ~FALSE equals TRUE

~ is written ! in some programming languages.

Implication  ⇒   -  pronounced implies, written => in TLA+

P => Q is true iff P is false and/or Q is true.  In other words:

TRUE => TRUE  equals TRUE        FALSE => TRUE equals TRUE
TRUE => FALSE equals FALSE       FALSE => FALSE equals TRUE

Propositional logic also has the equivalence relation  ≡ , written in TLA+ as <=>.  It is the equality relation on Booleans: If P and Q are Boolean values, then P <=> Q has the same meaning as P = Q.  However, it's a good idea to write P <=> Q instead of P = Q if P and Q should be Boolean-valued expressions, because TLC will raise an error when evaluating P <=> Q if they're not. 

Predicate Logic

Predicate logic allows us to write formulas of the following two forms:

\A i \in S : ...    meaning     For every element i of S : ... is true.

\E i \in S : ...    meaning     For some element i of S : ... is true.

Mathematicians call \A and \E quantifiers and write them  ∀  and  ∃ .

These operators are very important because they enormously expand the class of formulas we can write.  You may have seen them before in a math class, but you may not have learned how useful they can be in practice.  We'll see many examples of their use in algorithms.  Here, they are explained in terms of a simple mathematical concept: what it means for a number to be a prime. 

We write a formula that is true of an integer n iff n is a prime.  A prime is an integer greater than 1 whose only positive divisors are 1 and n.  Since a positive divisor of n must be in 1..n, an integer n is a prime iff it satisfies:

n > 1  and  n has no divisors in 2..(n-1)

We can write this with \A as

(n > 1)  /\  \A m \in 2..(n-1) : m does not divide n

(n > 1)  /\  \A m \in 2..(n-1) :  ~ (m divides n)

That m divides n means there exists a number p such that n equals m * p.  Since m is in 2..(n-1), such a p must also be in 2..(n-1). So, we can rewrite the assertion above as

(1)   (n > 1)  /\  \A m \in 2..(n-1) : ~ \E p \in 2..(n-1) : n = m * p

(I've numbered the formula so I can refer to it easily.)  If you find formulas like this intimidating, click here.

A natural number is prime iff formula (1) is true when we substitute that number for n.  For example, 79 is prime iff this formula equals TRUE:

(79 > 1)  /\  \A m \in 2..(79-1) : ~ \E p \in 2..(79-1) : 79 = m * p

Have TLC check this formula to see if 79 is a prime.  Let's try some other examples.  But to save typing, we first define an operator IsPrime so that for any number, say 373, IsPrime(373) equals the formula obtained from (1) by substituting 373 for n.  In the specification—that is, in module Session1—we put this definition:

IsPrime(n) ==    (n > 1)  
              /\ \A m \in 2..(n-1) : ~ \E p \in 2..(n-1) : n = m * p 

(The == is pretty-printed as .)  Copy the definition, open the tab labeled Session1, and paste the definition in the module.  Put it after the EXTENDS statement (you'll learn later what the statement is for) and before the ===...= line that ends the module.  Save the module, which you can do by pressing Control S.  Go back to the model's tab.  You can now have TLC check if 79 is a prime by typing IsPrime(79) in the Expression field.  Try checking some more numbers for primality.

Formula (1) makes an assertion about the value of n.  It says nothing about the values of m and p.  We get an equivalent formula (one making the same assertion about n) if we replace m and p by other identifiers—for example, by writing:

(2)   (n > 1)  /\  \A w \in 2..(n-1) : ~ \E d \in 2..(n-1) : n = w * d

We say that m and p are bound in formula (1), and that w and d are bound in formula (2).  A quantifier declares its bound variable within the quantifier's scope.  We also say that n is free in these formulas, meaning it's not bound in them.  TLA+ does not allow assigning a new meaning to an identifier that already has a meaning, so formula (2) cannot appear in a context in which w or d is declared or defined.

We can simplify formula (1).  The following equivalences should be obvious from the meanings of \A and \E. For example, the first is true because the statement it's not true that all elements of S satisfy some condition is equivalent to the statement it's true that some element of S does not satisfy the condition.

~ \A i \in S : ...    is equivalent to     \E i \in S : ~ (...)

~ \E i \in S : ...    is equivalent to     \A i \in S : ~ (...)

Using the second equivalence, we can rewrite formula (1) as

(n > 1)  /\  \A m \in 2..(n-1) : \A p \in 2..(n-1) : ~ (n = m * p)

which is equivalent to

(3)   (n > 1)  /\  \A m \in 2..(n-1) : \A p \in 2..(n-1) : n /= m * p

We can further simplify (3).  TLA+ allows the following abbreviations:

\A i \in S : \A j \in T : ...    abbr. as     \A i \in S, j \in T : ...

\A i \in S : \A j \in S : ...    abbr. as     \A i, j \in S : ...

These abbreviations apply to \E as well as \A.  Using the second abbreviation for \A, we can rewrite (3) as:

(4)   (n > 1)  /\  \A m, p \in 2..(n-1) : n /= m * p

The following exercise has nothing to do with algorithms, but it will give you practice expressing more complex concepts in terms of simpler ones—an important skill when writing algorithms. 

Exercise 2   Goldbach's conjecture states that every even integer greater than 2 is the sum of two primes.  No one has proved this conjecture or found a counterexample, and TLA+ won't change that.  This exercise is to state the conjecture mathematically—that is, write a formula that equals TRUE iff Goldbach's conjecture is true.  Click here to show a hint.  To show another hint, click here . 

TRUE versus True

A formula is a Boolean-valued expression, meaning that it equals either TRUE or FALSE.  For example, 2+n=4 is a formula; whether it equals TRUE or FALSE depends on the value of the identifier n.  Grammatically, a formula is a noun. However, people often write things like:

Everyone knows 2+2=4, but economists seem to believe 2+2=5.

Everyone knows 2+2 equals 4, but economists seem to believe
2+2=5 is true.