Session 3   A Simple Algorithm

1  Property Driven Development

We will now consider a very simple algorithm, one that actually computes something: the maximum of a tuple of numbers.  You may have heard about Property Driven Development (PDD).  Programmers typically start with a general idea of what a program should do and work out the details as they write the code.  The idea of PDD is that you should decide precisely what a program should do before writing the code that describes how the program does it.  The what are the properties the program's output should satisfy.

PDD helps avoid this mistake:

After writing a large part of the program, the programmer realizes her code doesn't handle some special case or satisfy some subtle property that it should.  She must then either throw away a lot of what she has done, or else correct the problem with ad hoc patches that produce an ugly, hard to maintain program.

PDD also aids in writing tests, because the properties that the program's output should satisfy are precisely what need to be tested.  I have been told that at Microsoft, the strongest advocates of writing those properties are the groups that test software.

PlusCal is well suited to PDD because we can check directly if the algorithm satisfies its required properties.  After writing the properties, there is no need to write (non-trivial) code to test that the algorithm satisfies them.

2  Computing the Max of a Tuple

2.1  Pre/Postconditions

• max must equal some inp[n]
• max must be greater than or equal to all inp[n]

      (\E n \in 1..Len(inp) : max = inp[n])   Why parentheses are needed.
   /\ (\A n \in 1..Len(inp) : max >= inp[n])  

Very often, we don't expect an algorithm to work for all conceivable inputs.  It needs to meet its goal only for inputs satisfying some condition.  To simplify our algorithm's task, let's suppose that we care only about input tuples whose values are greater than some number—say the number -99999.  This assumption is expressed as:

 
\A n \in 1..Len(inp) : inp[n] > -9999 

2.2  The Algorithm

Open the specification Session3.  This time, let's look at the module's first statement:

EXTENDS Integers, Sequences, TLC

Integers  Defines standard operators of arithmetic like + and =<, the integer interval operator .., and the sets Nat and Int.

Sequences  Defines operators on tuples (finite sequences) including Len.

TLC  Defines operators used in the TLA+ translation of some PlusCal statements, including print.

Nothing can come before an EXTENDS statement in the body of the module except comments.

Next comes a comment containing algorithm TupleMax.  The algorithm's variables statement declares the input and output variables inp and max and a variable i also used in the code.  The initial value of inp is an arbitrary tuple used to test the code.  We'll see later how to do more thorough testing.  Following the variables statement is an assert statement that checks the precondition.

The computation is done in the obvious way, examining the tuple elements inp[1], inp[2], etc. in order and keeping max equal to the largest value it has found.  If you're acquainted with popular programming languages, it will probably look familiar.  The standard way to write a loop in PlusCal is with a while statement.  The statement

while (test) { body }

The if statement has the general form

if (test) { if_body } else { else_body }

The complete algorithm is:

--algorithm TupleMax {
   variables inp = <<1, 3, 2>>,  max = -99999, i = 1 ;    
   { 
     assert  \A n \in 1..Len(inp) : inp[n] > -99999 ;
     while (i =< Len(inp)) {
       if (inp[i] > max) { max := inp[i] } ;
       i := i + 1
     } ;
     assert    (\E n \in 1..Len(inp) : max = inp[n])
            /\ (\A n \in 1..Len(inp) : max >= inp[n])  
   }
}

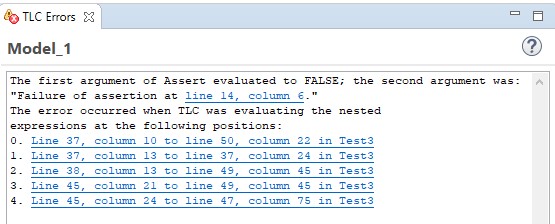
Clicking on line 14, column 6 takes you to the beginning of the assert statement in the code.  At the bottom of the message in the error window is a list of positions in the algorithm's TLA+ translation.  The last one is usually the most relevant one.  Clicking on it takes you to the part of the TLA+ translation whose execution caused the error.  But you don't want to look at the translation now.  You can go to the part of the PlusCal code that produced that part of the translation by pressing the F10 key.  You can go directly from the error window to the PlusCal code by control-clicking (holding down the control key when you click) on that line in the error message. 

The error message makes it pretty clear that the error was an assert statement whose expression was false.  It's not always so easy to figure out what caused the error TLC is reporting.  Going to the PlusCal code that was being evaluated when the error occurred can be a big help.

We have discovered that the code does not satisfy its postcondition for the input inp equal to << >> that satisfies the precondition.  So, we have to change the precondition to disallow that input, fix the code, or change the postcondition.  Which we do depends on what the code will be used for.  Since this is a toy example, it's not going to be used for anything.  So let's look at the possibilities and pick the one that's the most fun.

The simplest fix is to decide that the code doesn't have to handle that case.  We just add to the precondition the conjunct inp /= << >> or the conjunct Len(inp) > 0.  But that's no fun; it's too easy.

The alternative is to change the code and/or the postcondition.  Since we are already assuming that the elements of the tuple are greater than -99999, we can change the postcondition to require max to get the value -99999 if inp equals << >>.  We don't even have to change the code; that's what it already does.  We just have to modify the postcondition.  This can be done by replacing the assert statement that asserts the postcondition with an if statement (with an else clause) containing two assert statements.  One clause, executed when inp equals << >>, asserts max = -99999.  The other clause contains the current assert statement.  Do that now and have TLC check that it works—both for inp equal to << >> and equal to a couple of other tuples.  (Don't forget to save the file and run the translator each time before running TLC.)

It's more elegant to have the postcondition stated as an assert of a single formula. That formula can be written as

IF inp = << >> THEN max = -99999
               ELSE    (\E n \in 1..Len(inp) : max = inp[n])
                    /\ (\A n \in 1..Len(inp) : max >= inp[n])

The algorithm still contains some particular tuple used for testing as the initial value of inp.  We'll fix that below.

2.3  Declaring a Constant

The use of the arbitrary number -99999 in the algorithm is ugly.  And if the algorithm were not so trivial, it might not be clear that any sufficiently small number could be used instead.  It's better to replace -99999 by an unspecified integer.  Let's call it minValue.  Put the following statement in the Session3 module, after the EXTENDS statement and before the comment containing the algorithm.

CONSTANT minValue

ASSUME minValue \in Int

Modify the algorithm by substituting minValue for each of the three instances of -99999.  Save the module and run the translator.  Now let's check it.  Click on your model's tab.  It will probably open to the Model Checking Results sub-tab.  Whichever sub-tab it's on, there will be a link at the top saying 1 error detected.  Clicking on that link takes you to the Model Overview sub-tab.  Hovering the mouse over either of the two icons reveals the problem to be that you have to provide a value for the constant minValue. 

TLC can't check an algorithm containing a constant just knowing that it's an integer.  For it to check the algorithm, we have to tell it what value to use for minValue. We do this in the section of the sub-tab shown to the right.  Click on the Edit button, which raises a menu in which you can specify the value of minValue. 

That new window provides the three options shown to the left.  The Ordinary assignment option lets you enter any constant value you want for minValue in the window.  Let's set it to -99999.  Enter that value and click Finish (or type Control-Enter) to close the window.  Run TLC and check that you haven't introduced any error when making the changes.

3  Errors

We make lots of little errors when writing an algorithm, so let's take a closer look at TLC's error reports.  Just so we'll be working with exactly the same specification, open a new specification with module Session3a.  It contains a version of algorithm TupleMax that should be the same as the modified version of TupleMax now in your module Session3, except with the original initial value <<1,3,2>> for inp.  The specification should already contain the translation and a model named Model_1.  Open that model and run it to make sure everything is OK.

Now introduce an error by changing max >= inp[n] in the assert statement to max > inp[n].  Run the translator and run TLC on the model.  TLC should raise an error window reporting that the assertion is violated.

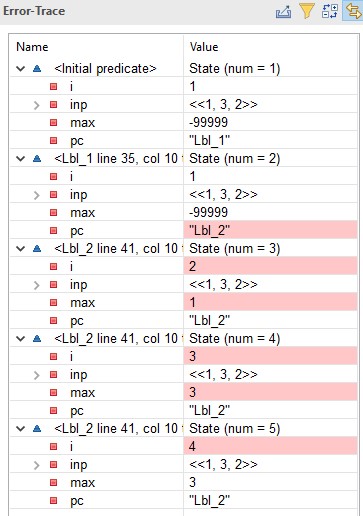This time, examine the error trace section of the window, which should look like the one shown here on the left.  The trace describes the execution of the algorithm as a sequence of 4 steps, where a step goes from one of the 5 states to the next.  A state is an assignment of values to variables.  (Values that have changed since the previous state are highlighted in pink.)  In addition to the three variables declared by the variables statement, there is a variable pc introduced by the TLA+ translation; you can ignore it for now.

The first step (from state number 1 to state number 2) represents the execution of the assert statement.  The second step represents a complete execution of one iteration of the while loop: evaluation of the test i =< Len(inp), execution of the if statement, and execution of the assignment to i.

TLA+ describes an execution of an algorithm as a sequence of steps.  How an execution is split into steps doesn't matter for the uniprocess algorithms we are now considering.  For efficiency, the translator by default splits them into the smallest number of steps it can.  What constitutes a step is a vital part of the description of a multiprocess algorithm.  You'll see later how steps are specified.  For now, the error trace and the locations reported in the error message should let you figure out what caused an error.  The error raised by the assert statement occurred when TLC was computing the state after the last one in the trace.  In this case, the last state in the trace was the one in which TLC was about to evaluate the while test with i = 4, and TLC executed the assert statement that raised the error while it was computing the next state.  TLC produces no error trace for an error that occurs when it is computing the initial values of the variables.

4  More Complete Testing

This version of algorithm TupleMax still contains an arbitrary initial value for inp. We could declare a new constant that we could use for that initial value.  We would test different inputs by changing the value assigned to the constant by the TLC model.  This algorithm is so simple that not much testing is required to convince ourselves that it's correct, so that's a reasonable approach.  But let's pretend that the algorithm is performing some difficult computation on tuples and we want to be sure it has no subtle error.  How would we test it?

The obvious approach is to test it on randomly chosen, realistic inputs.  These would be large tuples—especially if we expect the algorithm to be used with inputs that are tuples having millions of elements.  Some testing of large inputs might be necessary to ensure that the algorithm is efficient enough.  However, that's not a good way to look for inputs that satisfy the precondition and violate the postcondition.  To see why, consider this error one might make in the algorithm: writing < instead of =< in the while statement's test.  This causes an error only if the maximum element is the last one in the tuple.  We're much more likely to catch that error with a randomly chosen 3-tuple than with a randomly chosen 1000-tuple.

Instead of testing the algorithm with randomly chosen 1000-tuples, it would be better to test it with all possible 3-tuples.  We can't do that because there are an infinite number of integers, so there are an infinite number of 3-tuples of integers.  However, we can effectively test it for all 3-tuples by testing it on all 3-tuples with elements in a set of three different integers.  This is because the behavior of the algorithm depends only on whether an element of the tuple is greater than, less than, or equal to other elements, not on the actual values of the elements.  For example, algorithm TupleMax behaves the same with the inputs <<2, 8, 2>> and <<-7, 0, -7>> because both tuples have their first and third elements equal to each other and less than their second element.  Any error that occurs with a 3-tuple input will be found by choosing an arbitrary set of three integers and testing the algorithm on all 3-tuples whose elements belong to that set.  We'll now see how to write such a set of 3-tuples and get a PlusCal algorithm to use it.

4.1  Functions and Sets of Functions

As you've seen, a 3-tuple is an array with index set 1..3.  Mathematicians call an array a function, and they call its index set its domain.  I will use the mathematicians' terms because I want you to learn to think about algorithms mathematically.  (This will also let you think of arrays as only having elements numbered from 0, if you want to.)  But remember that TLA+ writes the value of the function f applied to the element e in its domain as f[e], not as f(e) the way mathematicians do.

The set of all functions having domain D and having values in a set S is written in TLA+ as [D -> S].  In other words, [D -> S] is the set of all functions f with domain D for which this is true:

\A i \in D : f[i] \in S

4.2  Initial Value Sets

If we want our algorithm to allow the initial value of inp to be any 3-tuple with elements in -3..-1, we just change the declaration of inp in the variables statement to:

inp \in [1..3 -> -3..-1]

We want to test the algorithm for additional tuples as well.  We could initialize inp to the set of all tuples we want to test it on.  However, if this were an algorithm that we wanted to show to other people, we would want to describe the set of all allowed initial values of inp.  Since the initial value of inp can be any tuple of integers, the variables declaration should allow inp to be any element in the set of all such tuples.  The set of all tuples with elements in a set S is written in TLA+ as Seq(S).  (Why Seq?)  So, we should write inp \in Seq(Int) in the variables declaration. 

However, TLC would then not be able to check the algorithm because it would allow infinitely many initial states.  It's possible to tell TLC to check it on only a finite subset of them, but doing that is a little complicated.  An easier approach is to define a constant that is assumed to be a set of tuples of integers and allow the initial value of inp to be any element of that set.  We can then tell TLC to substitute for that constant the set of initial values of inp for which we want to test the algorithm.  Let's call that constant Tuples. 

We can add another CONSTANT declaration for Tuples to the module, but I usually prefer to declare all constants at once.  So, change the existing declaration to:

CONSTANT minValue, Tuples

ASSUME (minValue \in Int) /\ (Tuples \subseteq Seq(Int))

We can now replace the precondition of the algorithm by an assumption about minValue. Instead of asserting that all the elements of inp are greater than minValue, we can require that all the elements of all the tuples in Tuples are greater than minValue.  We can do this by adding a condition to the ASSUME statement as follows:

ASSUME    (minValue \in Int) 
       /\ (\A t \in Tuples : \A i \in 1..Len(t) : t[i] > minValue)
       /\ (Tuples \subseteq Seq(Int))

ASSUME /\ (minValue \in Int) 
       /\ (\A t \in Tuples : \A i \in 1..Len(t) : t[i] > minValue)
       /\ (Tuples \subseteq Seq(Int))

ASSUME /\ minValue \in Int
       /\ \A t \in Tuples : \A i \in 1..Len(t) : t[i] > minValue
       /\ Tuples \subseteq Seq(Int)

assert IF inp = << >> THEN max = minValue
                      ELSE /\ \E n \in 1..Len(inp) : max = inp[n]
                           /\ \A n \in 1..Len(inp) : max >= inp[n]

Now let's test algorithm TupleMax on lots of tuples.  Save the file, run the translator, and open the model.  You will see that there is now an error in the model because the constant Tuples has not been assigned a value.  Go to the Model Overview sub-tab and double-click on Tuples in the What is the model section.  Copy and paste the following set of tuples as the value:

 [{1} -> {-1}] \cup [1..2 -> -2..-1] \cup [1..3 -> -3..-1]

Puzzle   How many different ways can you write the set containing only the
0-tuple << >>?  Show the answer.

\A i \in {} : f[i] \in S

Run TLC on the model again to make sure the algorithm still works for the empty tuple.  You can also change the while test to i < Len(inp) and check that TLC finds the error.

Project

You will write two algorithms by yourself.  Put each one in a new specification, which you create the same way you opened a specification in Section 2.1 of Session 1, except by browsing to any folder you want and entering a non-existing file name (with no extension) as the name of the specification.  For each algorithm, use our modified version of algorithm TupleMax from module Session3a as a template, copying its EXTENDS statement.  Do not try to open a model for a specification until you have written and successfully translated its algorithm.

Part 2.  The algorithm in Part 1 uses about n multiplications to compute m ^ n.  Write an algorithm that uses only about log₂n multiplications.  You will need to use these two TLA+ operators:

Integer Division  \div  (pretty-printed ÷)

m \div n is the largest integer less than or equal to m / n.  For example, 5 \div 2 equals 2 and (-5) \div 2 equals -3.  (But -5 \div 2 equals -(5 \div 2), which equals -2.)

Modulo  %

m % n is the non-negative remainder when the integer m is divided by the positive integer n.  For example, 5 % 2 and -5 % 2 both equal 1.  Thus, m % n equals 0 iff m is a multiple of n.

The precise definitions of these two operators make this formula true:

 \A m, n \in Int :
    (n > 0) => /\ m  =  n * (m \div n)  +  (m % n)
               /\ (0  =< m % n)  /\  (m % n < n)

Hint:   m ^ 13 = (m ^ 8) * (m ^ 4) * (m ^ 1)