Session 8   Mutual Exclusion

1  Introduction

1.1  The Problem

An atomic operation is one that is executed in a single step.  Algorithm Add2FGSem of Session 7 illustrates how a lock is used to make an operation to a shared resource appear atomic—in that example, the operation of incrementing the shared variable x.  In general, a set of processes sharing a resource may each repeatedly lock and unlock the resource, doing other things in between. 

The problem of implementing a lock with only atomic read and write operations was introduced and solved by the Dutch computer scientist Edsger W. Dijkstra in 1965, in a seminal paper that began the study of concurrent computing.  Instead of using the metaphor of locks, he called the part of a process's code in which the resource is locked the critical section.  He used the term noncritical section for the rest of the process's code—the part other than the critical section and the code used for locking and unlocking.  Instead of locking, he wrote of entering the critical section.  He described the requirement that at most one process can hold the lock as that of mutually exclusive access to the critical section.  Ever since, the problem of implementing a lock has been called the mutual exclusion problem.  A lock is also sometimes called a mutex.

In the mutual exclusion problem, each process performs this cyclic activity, 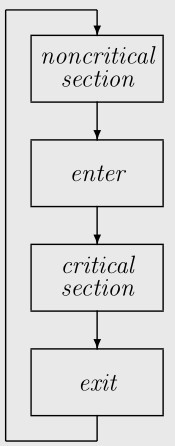where each box represents an operation that is not necessarily atomic.  In addition to mutual exclusion, the requirement that at most one process can be in its critical section, Dijkstra stated three other requirements for a solution that are relevant here.  A fourth requirement, not satisfied by his original solution, is also often added.  The first requirement is

Nothing may be assumed about execution speeds of the different processes, not even that they are constant.

1.2  A Warning

Modern computers are designed for speeding up uniprocess computations.  They freely reorder the execution of operations for efficiency if it doesn't affect the outcome of the computation—assuming no other process is accessing the memory at the same time.  That assumption may not be valid for a process in a multiprocess program. 

Because of this reordering of operations, a naive implementation of correct multiprocess PlusCal algorithms, including the mutual exclusion algorithms described here, can produce incorrect code.  Computers provide instructions to prevent unwanted reordering of code.  One of the skills required for multiprocess programming is knowing how and when to use those instructions.  This tutorial is about writing correct algorithms, not about coding those algorithms in a programming language.

The need for extra instructions in the code to prevent reordering makes most mutual exclusion algorithms, including the ones given here, unsuitable for implementing locks in most of today's applications.  However, mutual exclusion is a fundamental problem in computing.  New instances of the mutual exclusion problem can still arise that make currently impractical algorithms useful, or that require new algorithms.  One source of those instances is new hardware designs. 

The best reason to study mutual exclusion is that it provides a good introduction to concurrent algorithms.  It seems simple but is surprisingly difficult to solve.  Dijkstra published the first solution.  The second published attempt at a solution was wrong.  It's a fun problem.

2  The Algorithms

2.1  The Algorithms' Form

All our mutual exclusion algorithms will have the following form, where skip is a PlusCal statement that does nothing.

ncs: while (TRUE) {
        skip ;  \* represents the noncritical section
 enter: ...  ;
    cs: skip ;  \* represents the critical section
  exit: ... 
      }

We define a constant Procs to be the set of processes.  For simplicity, in this session I describe two-process mutual exclusion algorithms, where Procs equals {0,1}.  I leave their generalizations to an arbitrary number of processes as exercises. 

The basic property to be satisfied by a mutual exclusion algorithm is mutual exclusion: no two processes are in their critical sections at the same time.  This property is expressed by the invariance of the formula MutualExclusion, defined for two processes by:

MutualExclusion == ~ ((pc[0] = "cs") /\ (pc[1] = "cs"))

Exercise 1   Define MutualExclusion for an arbitrary set Procs of processes.  Show the answer.

MutualExclusion == \A i, j \in Procs : 
                      (i /= j) =>  ~ ((pc[i] = "cs") /\ (pc[j] = "cs"))

MutualExclusion == ~ \E i \in Procs : \E j \in Procs \ {i} : 
                                (pc[i] = "cs") /\ (pc[j] = "cs")

We are going to write a sequence of algorithms.  You could use a single specification and replace each algorithm with the next one.  You could also keep all the algorithms, making each one a separate specification in its own module.  I suggest keeping all the algorithms in a single specification, but deactivating all but one.  You can deactivate an algorithm by changing its beginning token—for example by putting a space after the -- in --algorithm or --fair algorithm. 

If you use a single specification, you might want to create a separate model for each algorithm.  That's easy to do with the Clone Model option on the TLC Model Checker menu in the Toolbox's top menu bar.

You can create the module or modules and the models that you need, using whatever names you want.  Just remember that if you create a new model before running the translator on some algorithm, you'll have to tell the model to use the temporal formula Spec as its behavior spec.

2.2  Algorithm Alternate

Our first algorithm simply allows two processes to alternately enter their critical sections, using a variable turn to indicate which process goes next.  It uses the PlusCal convention that in a process set's code, self equals the current process's id.  For any number i in {0,1}, the obvious way to write the other number in that set is (i+1) % 2.  The algorithm uses the observation that this other number can also be written 1-i.  It allows either process to enter its critical section first.

--algorithm Alternate {
  variable turn \in Procs ;
  process (p \in Procs) {
    ncs: while (TRUE) {
           skip ;
  enter:   await turn = self ;
     cs:   skip ;
   exit:   turn := 1 - self 
         }
  }  
}

It's obvious that mutual exclusion is satisfied by this algorithm because processes take turns entering the critical section.  But a better way to understand why it satisfies mutual exclusion is to ask, what is it about the state that prevents a process from entering the critical section when another process is already there?  In other words, what invariant does that algorithm maintain that prevents that from happening?  The answer is:

\A i \in Procs : (pc[i] = "cs") => (turn = i)

Mutual exclusion is trivially satisfied if the algorithm does nothing.  In addition to satisfying mutual exclusion, an algorithm should ensure that processes enter the critical section.  As we saw in Session 5, we need to add a directive to the algorithm to ensure that it does something.  We'll discuss how that's done later.  For now, we assume that a process keeps executing steps unless an await statement prevents it.  It's obvious that, with this assumption, the algorithm ensures that both processes keep entering and exiting their critical sections.

Exercise 2   Generalize algorithm Alternate to one in which N processes enter the critical section in cyclic order, where N is declared to be a CONSTANT in the module.  Show the answer.

Procs == 0..(N-1)

exit:   turn := (self + 1) % N

2.3  The 1-Bit Solution

Algorithm Alternate satisfies mutual exclusion of the two processes.  However, the second of Dijkstra's requirements for a solution is:

Any processes may take arbitrarily long to execute its noncritical section, and may even halt there.  Other processes must be able to enter the critical section without having to wait for those processes to complete the noncritical section.

Our next attempt at a solution is the following simple 2-process algorithm, in which each process i sets flag[i] to TRUE when it wants to enter the critical section and enters the critical section when it reads flag[1-i] equal to FALSE.

--algorithm 1BitProtocol {
    variables flag = [i \in Procs |-> FALSE] ;
    process (P \in Procs) {
     ncs: while (TRUE) {
            skip ; 
     enter: flag[self] := TRUE ; 
        e2: await ~ flag[1 - self] ;
        cs: skip ;
      exit: flag[self] := FALSE ;            
    }
  }
}

In an execution of the algorithm, flag[i] equals FALSE when process i is in its noncritical section.  This implies that if the other process is in its entry code, it will be able to execute its await statement e2 and enter the critical section.  Dijkstra's second requirement is therefore satisfied.  What about mutual exclusion?

Put the algorithm in a specification and run it with a model that checks if MutualExclusion is an invariant.  TLC reports that the algorithm deadlocks, with an error trace leading to the deadlocked state in which both processes i are at statement e2 with flag[i] equal to TRUE.

Obviously, a solution to the mutual exclusion problem should not deadlock.  But, does this protocol satisfy mutual exclusion?  Find out by unchecking the Deadlock box on the model's Model Overview sub-tab, which suppresses deadlock checking, and again running TLC to check if MutualExclusion is an invariant.  TLC should report that it is.

Why does the protocol satisfy mutual exclusion?  The obvious answer is: Both processes can't be in the critical section at the same time because if process i was the first to enter, then it must have set flag[i] to TRUE, which would have prevented process 1-i from entering.  But this is reasoning about the sequence in which things happen.  Remember that it's the current state that determines what an algorithm does next, so it does the right thing because of some property of the state—that is, because it maintains some invariant—not because of the sequence in which things happened.

Exercise 3   Write the invariant that explains why the protocol satisfies mutual exclusion.  Have TLC check that it is an invariant. Show the answer.

\A i \in Procs : /\ (pc[i] \in {"e2", "cs"}) => flag[i]
                 /\ (pc[i] = "cs") => (pc[1 - i] /= "cs")

There's a simple way to eliminate the deadlock in the protocol.  When the process is at e2, if it finds the other process's bit equal to TRUE, it doesn't wait for it to equal FALSE.  Instead, it sets its bit to FALSE and tries again by going back to enter.  The simplest way to write this algorithm is with the PlusCal goto statement.  The statement goto enter puts control in the process at label enter.  In the TLA+ translation, it simply sets pc[self] to "enter". (If you are shocked by the presence of a goto statement, read why the goto in PlusCal is not harmful.)  Here's the algorithm:

--algorithm 1BitNoDeadlock {
    variables flag = [i \in Procs |-> FALSE] ;
    process (P \in Procs) {
      ncs: while (TRUE) {
             skip ; 
      enter: flag[self] := TRUE ; 
         e2: if (flag[1 - self]) {              
         e3:   flag[self] := FALSE ;
               goto enter 
             } ;
         cs: skip ;
       exit: flag[self] := FALSE ;            
      }
    }
}

There exists no execution, no matter how improbable it may be, in which at some point a process is in the entry code but no process is ever in the critical section.

It may seem unlikely that the two processes livelock for very long, with neither of them entering the critical section.  In fact, a similar protocol has been used in ethernets and wifi systems, where the probability of livelock lasting very long is reduced by having each process wait a random length of time before re-executing the enter step.  However, unanticipated livelock can produce unexpected delays that significantly degrade performance.  We will see how TLC can be used to detect livelock, and how a PlusCal algorithm can indicate where care must be taken to eliminate livelock or ensure that it has a low enough probability of lasting too long.  Meanwhile, we will modify 1BitNoDeadlock so it doesn't livelock.

We eliminate the livelock of 1BitNoDeadlock by having one of the processes allow the other to enter if they are both in their entry code.  In particular, we have process 1 allow process 0 to enter by setting flag[1] to FALSE when it finds flag[0] equal to 0.  Here is the algorithm.

--algorithm 1BitMutex {
  variables flag = [i \in Procs |-> FALSE] ;
  process (P \in Procs) {
    ncs: while (TRUE) {
           skip ;
    enter: flag[self] := TRUE ; 
       e2: if (flag[1 - self]) {              
       e3:   if (self = 0) { goto e2 } 
             else {           
               flag[self] := FALSE ;
       e4:     await ~ flag[1 - self] ;
               goto enter ;              
              } 
           } ;
       cs: skip ;
     exit: flag[self] := FALSE            
    }
  }
}

Exercise 4   Algorithm 1BitMutex can be generalized to satisfy mutual exclusion with the set Procs of processes equal to 0..(N-1), for any positive integer N.  Each process i allows the processes in 0..(i-1) to enter the critical section before it by setting its flag to FALSE if it finds any of their flags equal to TRUE.  Write this algorithm and have TLC check that it satisfies mutual exclusion.  (Remember that a process should read at most one other process's flag in any step.)  If the translator says you need a label at a certain point, just add it.  Start by running TLC on models with N equal to 2 or 3.  Slowly increase N until you get tired of waiting for TLC to finish. Show the answer.

--algorithm 1BitNProcMutex {
  variables flag = [i \in Procs |-> FALSE] ;
  process (P \in Procs) 
  variable nxt = 0 ;
  { ncs: while (TRUE) {
           skip ;
    enter: flag[self] := TRUE ;
       e2: while (nxt /= self) {
             if (flag[nxt]) {
       e3:     flag[self] := FALSE ;
       e4:     await ~ flag[nxt] ;
               nxt := 0 ;
               goto enter
             }
             else { nxt := nxt + 1 }
           } ;
           nxt := self + 1 ;
       e5: while (nxt < N) {
             await ~ flag[nxt] ;
             nxt := nxt + 1 ;
           } ;          
       cs: skip ;
     exit: flag[self] := FALSE ;
            nxt := 0           
    }
  }
}

2.4  Peterson's Algorithm

Algorithm 1BitMutex and its N-process generalization of Exercise 4 satisfy the three conditions for a mutual exclusion algorithm stated so far.  There is a fourth condition that is usually required:

If no process remains forever in the critical section, then any process that begins executing the entry code eventually enters the critical section.

To obtain a starvation-free algorithm, we combine the idea of algorithm 1BitMutex with that of algorithm Alternate.  Algorithm 1BitMutex gives priority to process 0.  Algorithm Alternate gives absolute priority to the process whose id equals turn, where a process's exit code sets turn to the id of the other process.  We obtain a starvation-free algorithm by adding a variable turn whose value is changed the way Alternate changes it, and modifying 1BitMutex so it gives priority to the process whose id equals turn.  The resulting algorithm is a slightly modified version of one published by Gary Peterson in 1981.

--algorithm Peterson {
  variables flag = [i \in Procs |-> FALSE] , turn = 0 ;
  process (P \in Procs) {
    ncs: while (TRUE) {
           skip ; 
    enter: flag[self] := TRUE ; 
       e2: if (flag[1 - self]) {              
       e3:   if (self /= turn) {
       e4:     flag[self] := FALSE ;
               goto e3 
              } 
              else { goto enter }
           } ;
       cs: skip ;
     exit: flag[self] := FALSE ;
       x2: turn := 1 - self 
    }
  }
}

Exercise 5   You are to translate a typical pseudocode description of a multiprocess algorithm into PlusCal.  On 11 February 2021, the Wikipedia page for Peterson's algorithm contained the following description of a starvation-free mutual exclusion algorithm it calls the filter algorithm.  It calls the identifier level in its pseudocode an array of N variables level[0] through level[N-1].  (In PlusCal, as in mathematics, we call it a function-valued variable with domain 0..(N-1).)  Its assumption that the value of one of their variables is stored in an atomic register means that it can be read or written in a single step.

The filter algorithm generalizes Peterson's algorithm to N > 2 processes.  Instead of a Boolean flag, it requires an integer variable per process, stored in a single writer/multiple reader (SWMR) atomic register, and N-1 additional variables in similar registers.  The registers can be represented in pseudocode as arrays:

level : array of N integers
last_to_enter : array of N-1 integers

The level variables take on values up to N-1, each representing a distinct "waiting room" before the critical section.  Processes advance from one room to the next, finishing in room N-1 which is the critical section.  Specifically, to acquire a lock, process i executes:

i ← ProcessNo
for 𝓁 from 0 to N-1 exclusive
    level[i] ← 𝓁
    last_to_enter[𝓁] ← i
    while last_to_enter[𝓁] = i 
             and there exists k ≠ i, such that level[k] ≥ 𝓁
       wait

To release the lock upon exiting the critical section, process i sets level[i] to -1.