Session 5   Termination

1  Checking Termination

In this tutorial, we consider two correctness properties of a program that is supposed to compute a value and terminate: that it computes the correct value and that it terminates.  You have seen how to use an assert statement to check that an algorithm computes the correct value.  We now consider termination.

Open the specification Session5 in the Toolbox.  Its algorithm TupleMaxND is the same as the one in Session4, but the specification has a model in which the value of Tuples is the set containing only the single tuple <<1,2,3>>. 

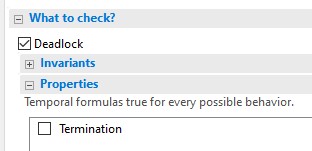Open that model and on the Model Overview tab, open the Properties part of the What to check? section.  As shown here, the default is not to check for termination.  Check the box next to Termination and run TLC on the model.  TLC raises an error window reporting that Temporal properties were violated.

As indicated on the screen shot, termination is the only temporal property.  So, algorithm TupleMaxND did not terminate.  The error trace indicates that the algorithm first examined inp[3], then inp[1], then inp[2].  Here is the end of the trace, showing that it ended in state number 4, in which I is empty and the algorithm is about to execute the while test from which it should reach the terminated state.  However, it didn't get there.  The mysterious state number 5 marked Stuttering indicates that the execution stopped and stayed forever in state number 4.  Why?

The question I would ask is, why did the execution get that far?  The answer is that, while TLC generally reports a shortest execution in which an algorithm terminates with the wrong answer, for uninteresting technical reasons it often does not report the shortest possible non-terminating execution.  Algorithm TupleMaxND actually allows an execution that remains forever in its initial state. 

This seems crazy.  Why doesn't PlusCal require that an algorithm keep going until it terminates (or deadlocks)?  This requirement is an example of a class of requirements called fairness conditions.  It is generally assumed without mention for uniprocess algorithms.  However, we don't always want to require it for multiprocess algorithms.  For example, consider an algorithm in which a client process issues requests to which a server process responds.  Requiring execution not to stop if the system hasn't terminated (or deadlocked) would mean that the client could never stop issuing requests, something we might not want to require.  So, we don't want this requirement to be the default.

We add the requirement to an algorithm by replacing the keyword --algorithm with --fair algorithm.  Do that and run TLC again.  (I will now stop reminding you that you have to save the specification and rerun the translator before you run TLC again—the Toolbox will remind you.)  TLC should report no error.

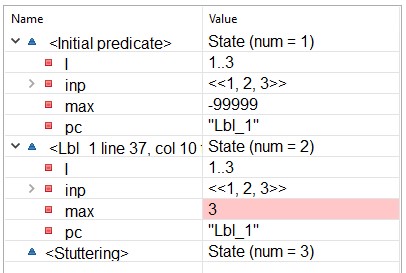Let's now make the algorithm run forever.  Comment out the statement I := I \ {i} (you can just type \* to its left), and run TLC.  As expected, TLC reports that the temporal property is violated.  This error trace shows that the algorithm first chose to examine inp[3], and then kept repeating that choice, remaining forever in the second state. 

2  TLC's State Graph

No execution of this modified version of TupleMaxND can terminate.  Every execution ends with an infinite number of stuttering steps in which the same state keeps being repeated forever.  However, there are an infinite number of such executions.  For example, the algorithm can examine inp[1] n times, for any number n, and then examine inp[3] forever.  Why doesn't TLC run forever examining all those executions?

The answer is that TLC does not compute executions; it computes reachable states.  More precisely it computes a graph whose nodes are all states that can occur in some execution and whose edges describe the possible transitions from one state to the next state.  Here is the graph for this algorithm, where the shaded node describes the initial state:

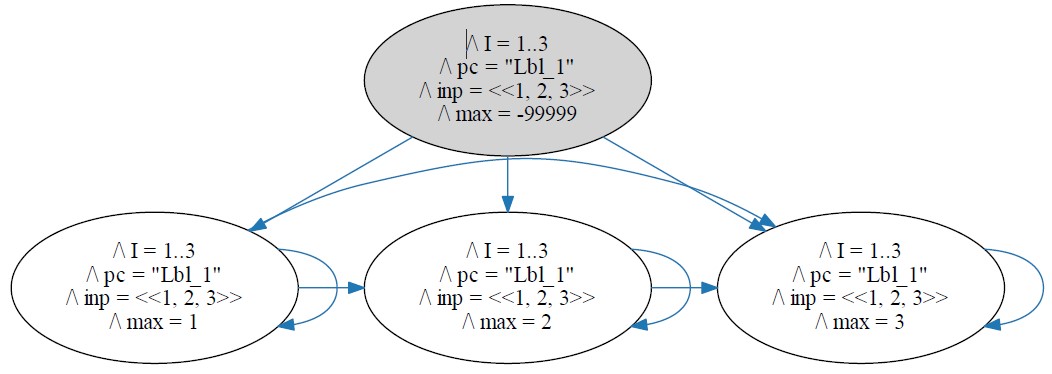
Here is the state graph for the original version of our algorithm, with the I := I \ {i} statement uncommented.  It should be clear, except for two things.  The first is the mysterious pc variable that will be explained later.  The second is the arrow from the bottom state to itself.  That state is the one the algorithm reaches when it terminates. 

Termination is halting when we want the algorithm to halt.  Deadlock is halting when we don't want it to halt.  Wanting does not appear in a mathematical view of an algorithm.  The transition from the terminating state to itself is added to the TLA+ translation of the algorithm so TLC doesn't consider termination to be deadlock.

For most algorithms, there are much too many reachable states for a picture of the state graph to be useful.  However, looking at a tiny state graph can help you understand PlusCal. 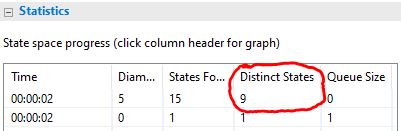 To find the number of reachable states TLC has found, look on the model's Model Checking Results tab at the top of the Distinct States column.  As shown here, it shows us that this version of TupleMaxND has 9 reachable states. 

If there are few enough states, you may want the Toolbox to display the state graph TLC constructs.  For that, you first have to download the Graphviz graph visualization program.  You then have to tell the Toolbox where you put that program.  Here's where to find out how to do that:  Click Help on the Toolbox's top menu bar, then click on the Table of Contents option.  Navigate as shown here to the help page for the TLC Options Page.  On that page, click on Features and scroll down to Visualize state graph after completion and follow the instructions there for where to enter the location of the downloaded GraphViz program.  (And after doing that, you might browse through the Toolbox's help pages to see what else is there.) 

To tell TLC to produce the state graph, check the obvious option on the Features section of the model's TLC Options sub-tab.  To raise that sub-tab, click on Additional TLC Options in the What to Check? section of the Model Overview sub-tab.