Session 6   Labels and the Translation

1  Labels

In TLA+, an execution of an algorithm is described as a sequence of states.  The change from one state to the next is called a step.  In the algorithms we've considered so far, execution of a single iteration of a while loop has occurred within a single step.  Why?  Why wasn't the execution of each assignment to a variable a separate step?  The answer is that we have let the translator decide what constitutes a step, and left to itself it makes steps as big as it can.

As we'll see in later sessions, what constitutes a single step is an important part of the definition of a multiprocess algorithm.  The translator shouldn't decide it; we need to specify it ourselves.  In PlusCal, what constitutes a step is described with labels.  From now on, we will add the labels ourselves instead of letting the translator decide where they should go.

Open the specification Session6 in the Toolbox.  The module declares a constant N that is assumed to be a natural number.  Next comes algorithm Square that sets x equal to the square of N, using the fact that N^2 equals the sum of the first N odd numbers.  (This is true for N equal to 0 if we define the sum of no numbers to equal 0.)

Algorithm Square has two labels: a labels the while statement, and b labels the assignment to x.  A step of an algorithm is the execution of the code from one label to the next, where there is an implicit label Done at the end of the algorithm.  There are rules about where a label must go and where it may not go.  The only ones that concern us now are: the body of the algorithm must begin with a label, and a while statement must be labeled.  For algorithm Square, label a satisfies both rules.  We'll encounter other rules later, but the translator is pretty good at explaining where an additional label is needed or why a label can't appear where you put it.

In any state, the value of the variable pc is the string that labels the next piece of code to be executed.  For example, in Square, when pc equals "b" the algorithm's next step will execute the assignment to x and set the value of pc to "a".  The value of pc equals the string "Done" when the algorithm has terminated.  When pc equals "a" or "b", we say that control is at a or b, respectively.

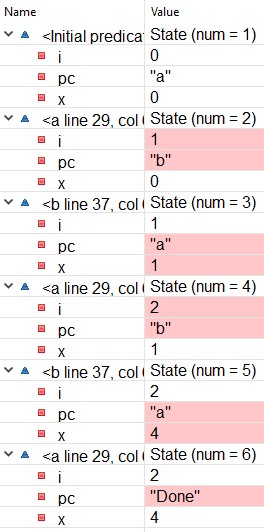
The specification has a model that assigns the value 2 to N.  That model is set up to report an error after the algorithm has terminated, so the error trace shows the entire execution.  (We'll see later how that's done.)  Run the model, ignoring the error message for now.  It should produce the error trace shown here. 

Read the trace and understand the details of each step.  Observe that the 1^st, 3^rd, and 5^th steps are a steps; and the 2^nd and 4^th steps are b steps. 

Now label the assignment to i as follows:

   c: i := i + 1 ;

Now remove the labels b and c, leaving only the label a, and run TLC.  This produces a trace with just 3 steps, all of them a steps.  The first 2 steps each execute one iteration of the while loop, including evaluation of its test and execution of its body.  The 3^rd step evaluates the while test and terminates because the test expression's value is FALSE. 

2  The TLA+ Translation

Let's now look at the TLA+ translation.  First, restore the original algorithm Square and its translation by putting back the label b on the assignment to x and running the translator.  Then run TLC to display the error trace describing the execution.

The translation of Square begins with the VARIABLES declaration, whose purpose should be obvious.  It next defines vars to equal the tuple of all the variables; vars is used below.

Next comes the definition of Init, which is a formula that describes the possible initial states of an execution.  For algorithm Square, the definition is

/\ x = 0
/\ i = 0
/\ pc = "a"

variables x = 0, i \in 0..3 ;

After the definition of Init come the parts of the translation that describe the steps that algorithm Square can take.  Thus far, I have been using the term step informally.  From now on, a step is defined to be any pair of states.  We say that the step starts in its first state and ends in its second state.  The translation now describes what steps are allowed to occur in an execution of the algorithm. 

Until the algorithm terminates, it can take steps that start with pc equal to either "a" or "b".  Those steps are described by the two formulas a and b that come next.  Let's look at the definition of b, which describes steps allowed by Square that start with pc equal to "b".

/\ pc = "b"
/\ x' = x + (2*i - 1)
/\ pc' = "a"
/\ i' = i

/\ "b" = "b"
/\ x' = 1 + (2*2 - 1)
/\ pc' = "a"
/\ i' = 2

/\ "b" = "b"
/\ 4 = 1 + (2*2 - 1)
/\ "a" = "a"
/\ 2 = 2

Any pair of states satisfying formula b is a b step.  There are infinitely many such steps—for example, there is one starting in a state with pc equal to "b", i equal to -374, and x equal to 42.  Only two of the infinitely many possible b steps occur in an execution of algorithm Square when N equals 2.  Check that the remaining three steps of the execution similarly satisfy formula a, so they are a steps.  Note that an a step can either leave pc equal to "a" or set it equal to "Done", depending on the value of i < N in the step's starting state.

Following the definitions of formulas a and b, the translation defines formula Terminating to equal

pc = "Done" /\ UNCHANGED vars

(x' = x) /\ (i' = i) /\ (pc' = pc)

The definitions that come next appear in translations of all PlusCal algorithms.  Formula Spec is a temporal logic formula that completely describes all possible executions of the algorithm.  If formula Spec is defined, then the Toolbox uses it as the default in the What is the behavior spec? section of a model's Model Overview when creating the model.  We run the translator before creating a model so Spec will be defined. 

If you change --algorithm to --fair algorithm, you will see that the definition of Spec has an additional conjunct.  That conjunct asserts that the algorithm must not stop unless it terminates or deadlocks.  Understanding how it asserts this requires a deeper understanding of TLA+ than you need to use PlusCal, so it won't be discussed here. 

The translation ends with the definition of formula Termination.  It is a temporal formula which asserts that the algorithm eventually terminates.  If it is defined in the module, the Toolbox adds it to the list of properties in the What to check? section, but does not select it to be checked, when it creates the model. 

3  Invariants

Instead of using an assert statement, we can use an invariant to check that an algorithm satisfies its postcondition.  An invariant of an algorithm is a formula that's true in all reachable states of the algorithm.  The postcondition algorithm Square should satisfy is x = N^2.  Satisfying a postcondition means that it is true when the algorithm terminates (if it terminates).  This is equivalent to saying that this condition is true for all states:

If the state is a terminated state, then the postcondition is true in that state.

(pc = "Done") => (x = N^2)

Look at the Invariants section of the What to check? section of the model's Model Overview tab.  It tells TLC to check the invariance of:

(pc = "Done") => (x /= N^2)

Edit the alleged invariant in the model to replace x /= N^2 with x = N^2, and run TLC to check that it now is an invariant.  Algorithm Square does satisfy its postcondition.

Exercise 1   Test the correctness of algorithm Square for a set of values of N as follows.  Create a new specification in the Toolbox by clicking on File in the top menu bar and selecting Open Spec then Add New Spec....  Copy into it the EXTENDS statement and algorithm Square from module Session6.  (To do this, you can open a new Toolbox editor on module Session6 with the Open module option on the File menu.)  Modify the algorithm to obtain a new algorithm named Square2 by making N a variable with some set of initial values.  Check that Square2 satisfies the invariant we have used to check the postcondition of algorithm Square.

You may have noticed that PlusCal does not require type declarations for variables.  In PlusCal, type correctness is an invariance property.  It's a useful property to check, since it quickly catches a lot of trivial errors.  In a conventional typed programming language, the variables x and i would have type Integer and pc would have type String.  It's good idea to define the type-correctness invariant in the module. I like to call it TypeOK, so add this definition after the algorithm's translation,

TypeOK == /\ x \in Int
          /\ i \in Int
          /\ pc \in STRING

TLA+ allows a more precise and useful type invariant than this.  For example, instead of just stating that the value of i is an integer, we can state that it's an integer from 0 through N.  Here is a better type-correctness invariant:

TypeOK == /\ x \in 0..N^2
          /\ i \in 0..N
          /\ pc \in {"a", "b", "Done"}

Invariance is arguably the most important concept in programming.  What an algorithm or a program does next depends only on its current state, not what it did in the past.  To understand why an algorithm is correct, we must understand at each point in its execution what it is about the current state that ensures it must produce a correct result.  That understanding is best expressed as an invariant. 

By definition, an invariant is true on all reachable states of the algorithm.  The invariant that provides the most information about an algorithm is one that is true only on its reachable states.  That invariant is usually too complicated to write down.  However, it can be written for the simple algorithms we've been looking at.  But even for them, it's not easy.  Before looking at the answer to the following exercise, check your answer by counting how many states are allowed by your invariant and comparing it with the number of reachable states TLC found.  (You saw how to find the number of reachable states here.)

Exercise 2   Define an invariant Inv of algorithm Square that is true only on reachable states of the algorithm.  (It doesn't matter whether you use the version of the algorithm in which N is a constant or a variable.)  Show the answer.

Inv == /\ TypeOK                       
       /\ (pc = "a") => (x = i^2)      
       /\ (pc = "b") => (x = (i-1)^2) /\ (i > 0)
       /\ (pc = "Done") => (x = N^2) /\ (i = N)

Inv == /\ i \in 0.. N
       /\ \/ (pc = "a") /\ (x = i^2)  
          \/ (pc = "b") /\ (x = (i-1)^2) /\ (i > 0)
          \/ (pc = "Done") /\ (x = N^2) /\ (i = N)

Most algorithms are too complicated to have a simple invariant that is true only on reachable states.  However, an algorithm is correct because it maintains a suitable invariant.  Learning to express an intuitive understanding of an algorithm's correctness with a formula whose invariance captures that understanding is not easy, but it makes one a better algorithm designer and therefore a better programmer.  This tutorial does not try to teach you that skill. 

4  Functions

We will now modify algorithm Square so that instead of setting x to equal N^2, it sets it to be a function with domain 0..N such that x[i] equals i^2 for all i in 0..N.

So far, the only functions we've been able to write explicitly are tuples, where a tuple t is a function with domain 1..Len(t).  We can write a function with domain D with the TLA+ expression

[i \in D |-> exp]

[j \in 0..N |-> j^2]

Exercise 3   Modify the algorithm as indicated above.  Modify the model's invariant so it checks that the new algorithm satisfies its postcondition and check that it's correct.  Show the answer.

variables x = [j \in 0..N |-> 0], i = 0 ;

b: x[i] := x[i-1] + (2*i - 1)

(pc = "Done") => (x = [j \in 0..N |-> j^2])

b == /\ pc = "b"
     /\ x'[i] = x[i-1] + (2*i - 1)]
     /\ pc' = "a"
     /\ i' = i

x' = [x EXCEPT ![i] = x[i-1] + (2*i - 1)]